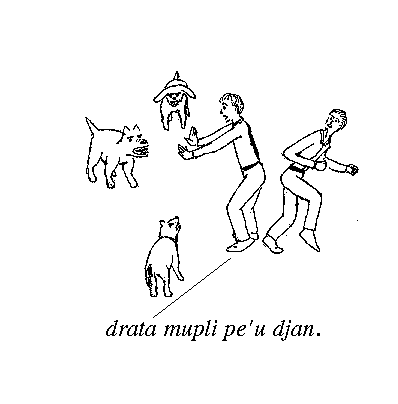The following brief dialogue is from Chapter 7 of Through The Looking Glass by Lewis Carroll.
“Who did you pass on the road?” the King went on, holding out his hand to the Messenger for some more hay.
“Quite right,” said the King: “this young lady saw him too. So of course Nobody walks slower than you.”
This nonsensical conversation results because the King insists on treating the word “nobody” as a name, a name of somebody. However, the essential nature of the English word “nobody” is that it doesn't refer to somebody; or to put the matter another way, there isn't anybody to which it refers.
The central point of contradiction in the dialogue arises in Example 16.3, when the King says “... Nobody walks slower than you”. This claim would be plausible if “Nobody” were really a name, since the Messenger could only pass someone who does walk more slowly than he. But the Messenger interprets the word “nobody” in the ordinary English way, and says (in Example 16.4) “... nobody walks much faster than I do” (i.e., I walk faster, or as fast as, almost everyone), which the King then again misunderstands. Both the King and the Messenger are correct according to their respective understandings of the ambiguous word “nobody/Nobody”.
There are Lojban words or phrases corresponding to the problematic English words “somebody”, “nobody”, “anybody”, “everybody” (and their counterparts “some/no/any/everyone” and “some/no/any/everything”), but they obey rules which can often be surprising to English-speakers. The dialogue above simply cannot be translated into Lojban without distortion: the name “Nobody” would have to be represented by a Lojban name, which would spoil the perfection of the wordplay. As a matter of fact, this is the desired result: a logical language should not allow two conversationalists to affirm “Nobody walks slower than the Messenger” and “Nobody walks faster than the Messenger” and both be telling the truth. (Unless, of course, nobody but the Messenger walks at all, or everyone walks at exactly the same speed.)
This chapter will explore the Lojban mechanisms that allow the correct and consistent construction of sentences like those in the dialogue. There are no new grammatical constructs explained in this chapter; instead, it discusses the way in which existing facilities that allow Lojban-speakers to resolve problems like the above, using the concepts of modern logic. However, we will not approach the matter from the viewpoint of logicians, although readers who know something of logic will discover familiar notions in Lojban guise.
Although Lojban is called a logical language, not every feature of it is “logical”. In particular, the use of le is incompatible with logical reasoning based on the description selbri, because that selbri may not truthfully apply: you cannot conclude from my statement that
that there really is a man; the only thing you can conclude is that there is one thing (or more) that I choose to refer to as a man. You cannot even tell which man is meant for sure without asking me (although communication is served if you already know from the context).
In addition, the use of attitudinals (see Chapter 13) often reduces or removes the ability to make deductions about the bridi to which those attitudinals are applied. From the fact that I hope George will win the election, you can conclude nothing about George's actual victory or defeat.
Let us consider, to begin with, a sentence that is not in the dialogue:
There are two plausible Lojban translations of Example 16.7. The simpler one is:
The cmavo zo'e indicates that a sumti has been omitted (indeed, even zo'e itself can be omitted in this case, as explained in Section 7.7) and the listener must fill in the correct value from context. In other words, Example 16.8 means “‘You-know-what’ sees me.”
However, Example 16.7 is just as likely to assert simply that there is someone who sees me, in which case a correct translation is:
Example 16.9 does not presuppose that the listener knows who sees the speaker, but simply tells the listener that there is someone who sees the speaker. Statements of this kind are called “existential claims”. (Formally, the one doing the seeing is not restricted to being a person; it could be an animal or – in principle – an inanimate object. We will see in Section 16.4 how to represent such restrictions.)
Example 16.9 has a two-part structure: there is the part da zo'u, called the prenex, and the part da viska mi, the main bridi. Almost any Lojban bridi can be preceded by a prenex, which syntactically is any number of sumti followed by the cmavo zo'u (of selma'o ZOhU). For the moment, the sumti will consist of one or more of the cmavo da, de, and di (of selma'o KOhA), glossed in the literal translations as “X”, “Y”, and “Z” respectively. By analogy to the terminology of symbolic logic, these cmavo are called “variables”.
Here is an example of a prenex with two variables:
In Example 16.10, the literal interpretation of the two variables da and de as “there-is-an-X” and “there-is-a-Y” tells us that there are two things which stand in the relationship that one loves the other. It might be the case that the supposed two things are really just a single thing that loves itself; nothing in the Lojban version of Example 16.10 rules out that interpretation, which is why the colloquial translation does not say “Somebody loves somebody else.” The things referred to by different variables may be different or the same. (We use “somebody” here rather than “something” for naturalness; lovers and beloveds are usually persons, though the Lojban does not say so.)
It is perfectly all right for the variables to appear more than once in the main bridi:
What Example 16.11 claims is fundamentally different from what Example 16.10 claims, because da prami da is not structurally the same as da prami de. However,
means exactly the same thing as Example 16.11; it does not matter which variable is used as long as they are used consistently.
It is not necessary for a variable to be a sumti of the main bridi directly:
is perfectly correct even though the da is used only in a possessive construction. (Possessives are explained in Section 8.7.)
It is very peculiar, however, even if technically grammatical, for the variable not to appear in the main bridi at all:
| da | zo'u | la | ralf. | gerku |
| There-is-an-X | such-that | that-named | Ralph | is-a-dog |
|
There is something such that Ralph is a dog. |
has a variable bound in a prenex whose relevance to the claim of the following bridi is completely unspecified.
What happens if we substitute “everything” for “something” in Example 16.7? We get:
Of course, this example is false, because there are many things which do not see the speaker. It is not easy to find simple truthful examples of so-called universal claims (those which are about everything), so bear with us for a while. (Indeed, some Lojbanists tend to avoid universal claims even in other languages, since they are so rarely true in Lojban.)
The Lojban translation of Example 16.15 is
When the variable cmavo da is preceded by ro, the combination means “For every X” rather than “There is an X”. Superficially, these English formulations look totally unrelated: Section 16.6 will bring them within a common viewpoint. For the moment, accept the use of ro da for “everything” on faith.
Here is a universal claim with two variables:
Again, X and Y can represent the same thing, so Example 16.17 does not mean “Everything loves everything else.” Furthermore, because the claim is universal, it is about every thing, not merely every person, so we cannot use “everyone” or “everybody” in the translation.
Note that ro appears before both da and de. If ro is omitted before either variable, we get a mixed claim, partly existential like those of Section 16.2, partly universal.
| da | ro | de | zo'u | da | viska | de |
| There-is-an-X | such-that-for-every | Y | : | X | sees | Y. |
|
Something sees everything. |
Example 16.18 and Example 16.19 mean completely different things. Example 16.18 says that for everything, there is something which it sees, not necessarily the same thing seen for every seer. Example 16.19, on the other hand, says that there is a particular thing which can see everything that there is (including itself). Both of these are fairly silly, but they are different kinds of silliness.
There are various possible translations of universal claims in English: sometimes we use “anybody/anything” rather than “everybody/everything”. Often it makes no difference which of these is used: when it does make a difference, it is a rather subtle one which is explained in Section 16.8.
The universal claims of Section 16.3 are not only false but absurd: there is really very little to be said that is both true and non-trivial about every object whatsoever. Furthermore, we have been glossing over the distinction between “everything” and “everybody” and the other pairs ending in “-thing” and “-body”. It is time to bring up the most useful feature of Lojban variables: the ability to restrict their ranges.
In Lojban, a variable da, de, or di may be followed by a poi relative clause in order to restrict the range of things that the variable describes. Relative clauses are described in detail in Chapter 8, but the kind we will need at present consist of poi followed by a bridi (often just a selbri) terminated with ku'o or vau (which can usually be elided). Consider the difference between
and
| da | poi | prenu | zo'u | da | viska | la | djim. |
| There-is-an-X | which | is-a-person | : | X | sees | that-named | Jim. |
|
Someone sees Jim. |
In Example 16.20, the variable da can refer to any object whatever; there are no restrictions on it. In Example 16.21, da is restricted by the poi prenu relative clause to persons only, and so da poi prenu translates as “someone.” (The difference between “someone” and “somebody” is a matter of English style, with no real counterpart in Lojban.) If Example 16.21 is true, then Example 16.20 must be true, but not necessarily vice versa.
Universal claims benefit even more from the existence of relative clauses. Consider
and
| ro | da | poi | gerku | zo'u | da | vasxu |
| For-every | X | which | is-a-dog | : | X | breathes. |
|
Every dog breathes. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Each dog breathes. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
All dogs breathe. |
Example 16.22 is a silly falsehood, but Example 16.23 is an important truth (at least if applied in a timeless or potential sense: see Section 10.19). Note the various colloquial translations “every dog”, “each dog”, and “all dogs”. They all come to the same thing in Lojban, since what is true of every dog is true of all dogs. “All dogs” is treated as an English plural and the others as singular, but Lojban makes no distinction.
If we make an existential claim about dogs rather than a universal one, we get:
It isn't really necessary for every Lojban bridi involving variables to have a prenex on the front. In fact, none of the examples we've seen so far required prenexes at all! The rule for dropping the prenex is simple: if the variables appear in the same order within the bridi as they did in the prenex, then the prenex is superfluous. However, any ro or poi appearing in the prenex must be transferred to the first occurrence of the variable in the main part of the bridi. Thus, Example 16.9 becomes just:
and Example 16.23 becomes:
You might well suppose, then, that the purpose of the prenex is to allow the variables in it to appear in a different order than the bridi order, and that would be correct. Consider
| ro | da | poi | prenu | ku'o | de |
| For-every | X | which | is-a-person, | there-is-a-Y |
| poi | gerku | ku'o | zo'u | de | batci | da |
| which | is-a-dog | : | Y | bites | X. |
The prenex of Example 16.27 is like that of Example 16.18 (but with relative clauses): it notes that the following bridi is true of every person with respect to some dog, not necessarily the same dog for each. But in the main bridi part, the de appears before the da. Therefore, the true translation is
If we tried to omit the prenex and move the ro and the relative clauses into the main bridi, we would get:
| de | poi | gerku | cu | batci | ro | da | poi | prenu |
| There-is-a-Y | which | is-a-dog | which-bites | every | X | which | is-a-person |
|
Some dog bites everyone. |
which has the structure of Example 16.19: it says that there is a dog (call him Fido) who bites, has bitten, or will bite every person that has ever existed! We can safely rule out Fido's existence, and say that Example 16.29 is false, while agreeing to Example 16.27.
Even so, Example 16.27 is most probably false, since some people never experience dogbite. Examples like Example 16.27 and Example 16.23 (might there be some dogs which never have breathed, because they died as embryos?) indicate the danger in Lojban of universal claims even when restricted. In English we are prone to say that “Everyone says” or that “Everybody does” or that “Everything is” when in fact there are obvious counterexamples which we are ignoring for the sake of making a rhetorical point. Such statements are plain falsehoods in Lojban, unless saved by a context (such as tense) which implicitly restricts them.
How can we express Example 16.27 in Lojban without a prenex? Since it is the order in which variables appear that matters, we can say:
| ro | da | poi | prenu | cu | se | batci | de | poi | gerku |
| Every | X | which | is-a-person | is-bitten-by | some-Y | which | is-a-dog. |
using the conversion operator se (explained in Section 5.11) to change the selbri batci (“bites”) into se batci (“is bitten by”). The translation given in Example 16.28 uses the corresponding strategy in English, since English does not have prenexes (except in strained “logician's English”). This implies that a sentence with both a universal and an existential variable can't be freely converted with se; one must be careful to preserve the order of the variables.
If a variable occurs more than once, then any ro or poi decorations are moved only to the first occurrence of the variable when the prenex is dropped. For example,
| di | poi | prenu | zo'u |
| There-is-a-Z | which | is-a-person | : |
| ti | xarci | di | di |
| this-thing | is-a-weapon | for-use-against-Z | by-Z |
|
This is a weapon for someone to use against himself/herself. |
(in which di is used rather than da just for variety) loses its prenex as follows:
As the examples in this section show, dropping the prenex makes for terseness of expression often even greater than that of English (Lojban is meant to be an unambiguous language, not necessarily a terse or verbose one), provided the rules are observed.
So far, we have seen variables with either nothing in front, or with the cmavo ro in front. Now ro is a Lojban number, and means “all”; thus ro prenu means “all persons”, just as re prenu means “two persons”. In fact, unadorned da is also taken to have an implicit number in front of it, namely su'o, which means “at least one”. Why is this? Consider Example 16.9 again, this time with an explicit su'o:
From this version of Example 16.9, we understand the speaker's claim to be that of all the things that there are, at least one of them sees him or her. The corresponding universal claim, Example 16.16, says that of all the things that exist, every one of them can see the speaker.
Any other number can be used instead of ro or su'o to precede a variable. Then we get claims like:
This means that exactly two things, no more or less, saw the speaker on the relevant occasion. In English, we might take “Two things see me” to mean that at least two things see the speaker, but there might be more; in Lojban, though, that claim would have to be made as:
which would be false if nothing, or only one thing, saw the speaker, but not otherwise. We note the su'o here meaning “at least”; su'o by itself is short for su'opa where pa means “one”, as is explained in Section 18.9.
The prenex may be removed from Example 16.34 and Example 16.35 as from the others, leading to:
and
respectively, subject to the rules prescribed in Section 16.5.
Now we can explain the constructions ro prenu for “all persons” and re prenu for “two persons” which were casually mentioned at the beginning of this Section. In fact, ro prenu, a so-called “indefinite description”, is shorthand for ro DA poi prenu, where “DA” represents a fictitious variable that hasn't been used yet and will not be used in future. (Even if all three of da, de, and di have been used up, it does not matter, for there are ways of getting more variables, discussed in Section 16.14.) So in fact
is short for
which in turn is short for:
Note that when we move more than one variable to the prenex (along with its attached relative clause), we must make sure that the variables are in the same order in the prenex as in the bridi proper.
Let us consider a sentence containing two quantifier expressions neither of which is ro or su'o (remembering that su'o is implicit where no explicit quantifier is given):
The question raised by Example 16.41 is, does each of the dogs bite the same two men, or is it possible that there are two different men per dog, for six men altogether? If the former interpretation is taken, the number of men involved is fixed at two; but if the latter, then the speaker has to be taken as saying that there might be any number of men between two and six inclusive. Let us transform Example 16.41 step by step as we did with Example 16.38:
(Note that we need separate variables da and de, because of the rule that says each indefinite description gets a variable never used before or since.)
| ci | da | poi | gerku | ku'o | re | de | poi | nanmu | zo'u |
| For-three | Xes | which | are-dogs | -, | for-two | Ys | which | are-men | : |
| da | batci | de |
| X | bites | Y. |
Here we see that indeed each of the dogs is said to bite two men, and it might be different men each time; a total of six biting events altogether.
How then are we to express the other interpretation, in which just two men are involved? We cannot just reverse the order of variables in the prenex to
| re | de | poi | nanmu | ku'o | ci | da | poi | gerku | zo'u |
| For-two | Ys | which | are-men | -, | for-three | Xes | which | are-dogs, | : |
| da | batci | de |
| X | bites | Y. |
for although we have now limited the number of men to exactly two, we end up with an indeterminate number of dogs, from three to six. The distinction is called a “scope distinction”: in Example 16.42, ci gerku is said to have wider scope than re nanmu, and therefore precedes it in the prenex. In Example 16.44 the reverse is true.
The solution is to use a termset, which is a group of terms either joined by ce'e (of selma'o CEhE) between each term, or else surrounded by nu'i (of selma'o NUhI) on the front and nu'u (of selma'o NUhU) on the rear. Terms (which are either sumti or sumti prefixed by tense or modal tags) that are grouped into a termset are understood to have equal scope:
| ci | gerku | ce'e | re | nanmu | cu | batci | ||
| nu'i | ci | gerku | re | nanmu | [nu'u] | cu | batci | |
| Three | dogs | [plus] | two | men, | bite. |
which picks out two groups, one of three dogs and the other of two men, and says that every one of the dogs bites each of the men. The second Lojban version uses forethought; note that nu'u is an elidable terminator, and in this case can be freely elided.
What about descriptors, like ci lo gerku, le nanmu or re le ci mlatu? They too can be grouped in termsets, but usually need not be, except for the lo case which functions like the case without a descriptor. Unless an actual quantifier precedes it, le nanmu means ro le nanmu, as is explained in Section 6.7. Two sumti with ro quantifiers are independent of order, so:
means that each of the dogs specified bites each of the men specified, for six acts of biting altogether. However, if there is an explicit quantifier before le other than ro, the problems of this section reappear.
Using the facilities already discussed, a plausible translation might be
| ro | da | poi | klama | le | zarci | cu | cadzu | le | foldi |
| All | X | such-that-it | goes-to | the | store | walks-on | the | field. |
|
Everyone who goes to the store walks across the field. |
But there is a subtle difference between Example 16.47 and Example 16.48. Example 16.48 tells us that, in fact, there are people who go to the store, and that they walk across the field. A sumti of the type ro da poi klama requires that there are things which klama: Lojban universal claims always imply the corresponding existential claims as well. Example 16.47, on the other hand, does not require that there are any people who go to the store: it simply states, conditionally, that if there is anyone who goes to the store, he or she walks across the field as well. This conditional form mirrors the true Lojban translation of Example 16.47:
| ro | da | zo'u | da | go | klama | le | zarci |
| For-every | X | : | X | if-and-only-if | it-is-a-goer-to | the | store |
| gi | cadzu | le | foldi |
| is-a-walker-on | the | field. |
Although Example 16.49 is a universal claim as well, its universality only implies that there are objects of some sort or another in the universe of discourse. Because the claim is conditional, nothing is implied about the existence of goers-to-the-store or of walkers-on-the-field, merely that any entity which is one is also the other.
There is another use of “any” in English that is not universal but existential. Consider
Example 16.50 does not at all mean that I need every box bigger than this one, for indeed I do not; I require only one box. But the naive translation
does not work either, because it asserts that there really is such a box, as the prenex paraphrase demonstrates:
| da | poi | tanxe | gi'e | bramau | ti | zo'u | mi | nitcu | da |
| There-is-an-X | which | is-a-box | and | is-bigger-than | this | : | I | need | X. |
What to do? Well, the x2 place of nitcu can be filled with an event as well as an object, and in fact Example 16.51 can also be paraphrased as:
| mi | nitcu | lo | nu | mi | ponse | lo | tanxe |
| I | need | an | event-of | I | possess | some | box(es) |
| poi | bramau | ti |
| which-are | bigger-than | this-one. |
Rewritten using variables, Example 16.53 becomes
| mi | nitcu | lo | nu | da | zo'u |
| I | need | an | event-of | there-being-an-X | such-that: |
| da | se | ponse | mi |
| X | is-possessed-by | me |
| gi'e | tanxe | gi'e | bramau | ti |
| and | is-a-box | and | is-bigger-than | this-thing. |
So we see that a prenex can be attached to a bridi that is within a sentence. By default, a variable always behaves as if it is bound in the prenex which (notionally) is attached to the smallest enclosing bridi, and its scope does not extend beyond that bridi. However, the variable may be placed in an outer prenex explicitly:
| da | poi | tanxe | gi'e | bramau | ti | zo'u |
| There-is-an-X | which | is-a-box | and | is-bigger-than | this-one | such-that: |
| mi | nitcu | le | nu | mi | ponse | da |
| I | need | the | event-of | my | possessing | X. |
But what are the implications of Example 16.53 and Example 16.55? The main difference is that in Example 16.55, the da is said to exist in the real world of the outer bridi; but in Example 16.53, the existence is only within the inner bridi, which is a mere event that need not necessarily come to pass. So Example 16.55 means
which is what Example 16.52 says, whereas Example 16.53 turns out to be an effective translation of our original Example 16.47. So uses of “any” that aren't universal end up being reflected by variables bound in the prenex of a subordinate bridi.
This section, as well as Section 16.10 through Section 16.12, are in effect a continuation of Chapter 15, introducing features of Lojban negation that require an understanding of prenexes and variables. In the examples below, “there is a Y” and the like must be understood as “there is at least one Y, possibly more”.
As explained in Section 15.2, the negation of a bridi is usually accomplished by inserting na at the beginning of the selbri:
| mi | na | klama | le | zarci |
| I | [false] | go-to | the | store. |
|
It is false that I go to the store. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
I don't go to the store. |
The other form of bridi negation is expressed by using the compound cmavo naku in the prenex, which is identified and compounded by the lexer before looking at the sentence grammar. In Lojban grammar, naku is then treated like a sumti. In a prenex, naku means precisely the same thing as the logician's “it is not the case that” in a similar English context. (Outside of a prenex, naku is also grammatically treated as a single entity – the equivalent of a sumti – but does not have this exact meaning; we'll discuss these other situations in Section 16.11.)
To represent a bridi negation using a prenex, remove the na from before the selbri and place naku at the left end of the prenex. This form is called “external bridi negation”, as opposed to “internal bridi negation” using na. The prenex version of Example 16.57 is
| naku | zo'u | la | djan. | klama |
| It-is-not-the-case-that | : | that-named | John | comes. |
|
It is false that: John comes. |
However, naku can appear at other points in the prenex as well. Compare
| naku | de | zo'u | de | zutse |
| It-is-not-the-case-that: | for-some-Y | : | Y | sits. |
| It-is-false-that: | for-at-least-one-Y | : | Y | sits. |
|
It is false that something sits. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Nothing sits. |
with
| su'ode | naku | zo'u | de | zutse |
| For-at-least-one-Y, | it-is-false-that | : | Y | sits. |
|
There is something that doesn't sit. |
The relative position of negation and quantification terms within a prenex has a drastic effect on meaning. Starting without a negation, we can have:
| roda | su'ode | zo'u | da | prami | de |
| For-every-X, | there-is-a-Y, | such-that | X | loves | Y. |
|
Everybody loves at least one thing (each, not necessarily the same thing). |
or:
| su'ode | roda | zo'u | da | prami | de |
| There-is-a-Y, | such-that-for-each-X | : | X | loves | Y. |
|
There is at least one particular thing that is loved by everybody. |
The simplest form of bridi negation to interpret is one where the negation term is at the beginning of the prenex:
| naku | roda | su'ode | zo'u | da | prami | de |
| It-is-false-that: | for-every-X, | there-is-a-Y, | such-that: | X | loves | Y. |
|
It is false that: everybody loves at least one thing. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
(At least) someone doesn't love anything. |
the negation of Example 16.61, and
| naku | su'ode | roda | zo'u | da | prami | de | |
| It-is-false-that: | there-is-a-Y | such-that | for-each-X | : | X | loves | Y. |
|
It is false that: there is at least one thing that is loved by everybody. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
There isn't any one thing that everybody loves. |
the negation of Example 16.62.
The rules of formal logic require that, to move a negation boundary within a prenex, you must “invert any quantifier” that the negation boundary passes across. Inverting a quantifier means that any ro (all) is changed to su'o (at least one) and vice versa. Thus, Example 16.63 and Example 16.64 can be restated as, respectively:
| su'oda | naku | su'ode | zo'u | da | prami | de |
| For-some-X, | it-is-false-that: | there-is-a-Y | such-that: | X | loves | Y. |
|
There is somebody who doesn't love anything. |
and:
| rode | naku | roda | zo'u | da | prami | de |
| For-every-Y, | it-is-false-that: | for-every-X | : | X | loves | Y. |
|
For each thing, it is not true that everybody loves it. |
Another movement of the negation boundary produces:
| su'oda | rode | naku | zo'u | da | prami | de |
| There-is-an-X | such-that-for-every-Y, | it-is-false-that | : | X | loves | Y. |
|
There is someone who, for each thing, doesn't love that thing. |
and
| rode | su'oda | naku | zo'u | da | prami | de |
| For-every-Y, | there-is-an-X, | such-that-it-is-false-that | : | X | loves | Y. |
|
For each thing there is someone who doesn't love it. |
Investigation will show that, indeed, each transformation preserves the meanings of Example 16.63 and Example 16.64.
The quantifier no (meaning “zero of”) also involves a negation boundary. To transform a bridi containing a variable quantified with no, we must first expand it. Consider
| noda | rode | zo'u | da | prami | de |
| There-is-no-X, | for-every-Y, | such-that | X | loves | Y. |
|
Nobody loves everything. |
which is negated by:
| naku | noda | rode | zo'u | da | prami | de |
| It-is-false-that: | there-is-no-X-that, | for-every-Y | : | X | loves | Y. |
|
It is false that there is nobody who loves everything. |
We can simplify Example 16.70 by transforming the prenex. To move the negation phrase within the prenex, we must first expand the no quantifier. Thus “for no x” means the same thing as “it is false for some x”, and the corresponding Lojban noda can be replaced by naku su'oda. Making this substitution, we get:
| naku | naku | su'oda |
| It-is-false-that | it-is-false-that | there-is-some-X-such-that |
| …rode | zo'u | da | prami | de |
| for-every-X | : | X | loves | Y |
|
It is false that it is false that: for an X, for every Y: X loves Y. |
Adjacent pairs of negation boundaries in the prenex can be dropped, so this means the same as:
| su'oda | rode | zo'u | da | prami | de |
| There-is-an-X-such-that, | for-every-Y | : | X | loves | Y. |
|
At least one person loves everything. |
which is clearly the desired contradiction of Example 16.69.
The interactions between quantifiers and negation mean that you cannot eliminate double negatives that are not adjacent. You must first move the negation phrases so that they are adjacent, inverting any quantifiers they cross, and then the double negative can be eliminated.
A complete discussion of logical connectives appears in Chapter 14. What is said here is intentionally quite incomplete and makes several oversimplifications.
A logical connective is a cmavo or compound cmavo. In this chapter, we will make use of the logical connectives “and” and “or” (where “or” really means “and/or”, “either or both”). The following simplified recipes explain how to make some logical connectives:
-
To logically connect two Lojban sumti with “and”, put them both in the bridi and separate them with the cmavo e.
-
To logically connect two Lojban bridi with “and”, replace the regular separator cmavo i with the compound cmavo .ije.
-
To logically connect two Lojban sumti with “or”, put them both in the bridi and separate them with the cmavo a.
-
To logically connect two Lojban bridi with “or”, replace the regular separator cmavo i with the compound cmavo .ija.
More complex logical connectives also exist; in particular, one may place na before e or a, or between i and je or ja; likewise, one may place nai at the end of a connective. Both na and nai have negative effects on the sumti or bridi being connected. Specifically, na negates the first or left-hand sumti or bridi, and nai negates the second or right-hand one.
Whenever a logical connective occurs in a sentence, that sentence can be expanded into two sentences by repeating the common terms and joining the sentences by a logical connective beginning with i. Thus the following sentence:
can be expanded to:
| mi | klama | ti | .ije | do | klama | ti |
| I | come-to | this-here | and | you | come-to | this-here |
|
I come here, and, you come here. |
The same type of expansion can be performed for any logical connective, with any valid combination of na or nai attached. No change in meaning occurs under such a transformation.
Clearly, if we know what negation means in the expanded sentence forms, then we know what it means in all of the other forms. But what does negation mean between sentences?
The mystery is easily solved. A negation in a logical expression is identical to the corresponding bridi negation, with the negator placed at the beginning of the prenex. Thus:
expands to:
and then into prenex form as:
| roda | zo'u | mi | prami | da | .ije |
| For-each-thing | : | I | love | it, | and |
| naku | zo'u | do | prami | da |
| it-is-false-that | : | you | love | (the-same)-it. |
|
For each thing: I love it, and it is false that you love (the same) it. |
By the rules of predicate logic, the ro quantifier on da has scope over both sentences. That is, once you've picked a value for da for the first sentence, it stays the same for both sentences. (The da continues with the same fixed value until a new paragraph or a new prenex resets the meaning.)
Thus the following example has the indicated translation:
| su'oda | zo'u | mi | prami | da |
| For-at-least-one-thing | : | I | love | that-thing. |
| .ije | naku | zo'u | do | prami | da |
| And | it-is-false-that | : | you | love | that-(same)-thing. |
|
There is something that I love that you don't. |
If you remember only two rules for prenex manipulation of negations, you won't go wrong:
-
Within a prenex, whenever you move naku past a bound variable (da, de, di, etc.), you must invert the quantifier.
-
A na before the selbri is always transformed into a naku at the left-hand end of the prenex, and vice versa.
Let us consider the English sentence
We cannot express this directly with na; the apparently obvious translation
| su'oda | poi | verba |
| At-least-one-X | which-are | child(ren) |
| na | klama | su'ode | poi | ckule |
| [false] | go-to | at-least-one-Y | which-are | school(s). |
when converted to the external negation form produces:
| naku | zo'u | su'oda | poi | verba | cu |
| It-is-false | that | some-which | are | children |
| klama | su'ode | poi | ckule |
| go-to | some-which | are | schools. |
|
All children don't go to some school (not just some children). |
Lojban provides a negation form which more closely emulates natural language negation. This involves putting naku before the selbri, instead of a na. naku is clearly a contradictory negation, given its parallel with prenex bridi negation. Using naku, Example 16.79 can be expressed as:
| su'oda | poi | verba | naku | klama | su'ode | poi | ckule |
| Some | which-are | children | don't | go-to | some | which-are | schools. |
|
Some children don't go to a school. |
Although it is not technically a sumti, naku can be used in most of the places where a sumti may appear. We'll see what this means in a moment.
When you use naku within a bridi, you are explicitly creating a negation boundary. As explained in Section 16.9, when a prenex negation boundary expressed by naku moves past a quantifier, the quantifier has to be inverted. The same is true for naku in the bridi proper. We can move naku to any place in the sentence where a sumti can go, inverting any quantifiers that the negation boundary crosses. Thus, the following are equivalent to Example 16.82 (no good English translations exist):
| su'oda | poi | verba | cu | klama | rode | poi | ckule | naku |
|
For some children, for every school, they don't go to it. |
In Example 16.83, we moved the negation boundary rightward across the quantifier of de, forcing us to invert it. In Example 16.85 we moved the negation boundary across the quantifier of da, forcing us to invert it instead. Example 16.84 merely switched the selbri and the negation boundary, with no effect on the quantifiers.
The same rules apply if you rearrange the sentence so that the quantifier crosses an otherwise fixed negation. You can't just convert the selbri of Example 16.82 and rearrange the sumti to produce
or rather, Example 16.86 means something completely different from Example 16.82. Conversion with se under naku negation is not symmetric; not all sumti are treated identically, and some sumti are not invariant under conversion. Thus, internal negation with naku is considered an advanced technique, used to achieve stylistic compatibility with natural languages.
It isn't always easy to see which quantifiers have to be inverted in a sentence. Example 16.82 is identical in meaning to:
but in Example 16.87, the bound variables da and de have been hidden.
It is trivial to export an internal bridi negation expressed with na to the prenex, as we saw in Section 16.9; you just move it to the left end of the prenex. In comparison, it is non-trivial to export a naku to the prenex because of the quantifiers. The rules for exporting naku require that you export all of the quantified variables (implicit or explicit) along with naku, and you must export them from left to right, in the same order that they appear in the sentence. Thus Example 16.82 goes into prenex form as:
| su'oda | poi | verba | ku'o | naku |
| For-some-X | which | is-a-child, | it-is-not-the-case-that |
| su'ode | poi | ckule | zo'u | da | klama | de | |
| there-is-a-Y | which | is-a-school | such-that: | X | goes | to | Y. |
We can now move the naku to the left end of the prenex, getting a contradictory negation that can be expressed with na:
| naku | roda | poi | verba |
| It-is-not-the-case-that | for-all-X's | which-are | children, |
| su'ode | poi | ckule | zo'u | da | klama | de |
| there-is-a-Y | which-is | a-school | such-that: | X | goes-to | Y. |
from which we can restore the quantified variables to the sentence, giving:
| naku | zo'u | roda | poi | verba | cu | klama | su'ode | poi | ckule |
|
It is not the case that all children go to some school. |
or more briefly
As noted in Section 16.5, a sentence with two different quantified variables, such as Example 16.91, cannot always be converted with se without first exporting the quantified variables. When the variables have been exported, the sentence proper can be converted, but the quantifier order in the prenex must remain unchanged:
| roda | poi | verba | su'ode |
| for-all-X's | which-are | children, | there-is-a-Y |
| poi | ckule | zo'u | de | na | se | klama | da |
| which | is-a-school | such-that: | Y | is-gone-to-by | X. |
While you can't freely convert with se when you have two quantified variables in a sentence, you can still freely move sumti to either side of the selbri, as long as the order isn't changed. If you use na negation in such a sentence, nothing special need be done. If you use naku negation, then quantified variables that cross the negation boundary must be inverted.
Clearly, if all of Lojban negation was built on naku negation instead of na negation, logical manipulation in Lojban would be as difficult as in natural languages. In Section 16.12, for example, we'll discuss DeMorgan's Law, which must be used whenever a sumti with a logical connection is moved across a negation boundary.
Since naku has the grammar of a sumti, it can be placed almost anywhere a sumti can go, including be and bei clauses; it isn't clear what these mean, and we recommend avoiding such constructs.
You can put multiple naku compounds in a sentence, each forming a separate negation boundary. Two adjacent naku compounds in a bridi are a double negative and cancel out:
Other expressions using two naku compounds may or may not cancel out. If there is no quantified variable between them, then the naku compounds cancel.
Negation with internal naku is clumsy and non-intuitive for logical manipulations, but then, so are the natural language features it is emulating.
DeMorgan's Law states that when a logical connective between terms falls within a negation, then expanding the negation requires a change in the connective. Thus (where “p” and “q” stand for terms or sentences) “not (p or q)” is identical to “not p and not q”, and “not (p and q)” is identical to “not p or not q”. The corresponding changes for the other two basic Lojban connectives are: “not (p equivalent to q)” is identical to “not p exclusive-or not q”, and “not (p whether-or-not q)” is identical to both “not p whether-or-not q” and “not p whether-or-not not q”. In any Lojban sentence having one of the basic connectives, you can substitute in either direction from these identities. (These basic connectives are explained in Chapter 14.)
The effects of DeMorgan's Law on the logical connectives made by modifying the basic connectives with nai, na and se can be derived directly from these rules; modify the basic connective for DeMorgan's Law by substituting from the above identities, and then, apply each nai, na and se modifier of the original connectives. Cancel any double negatives that result.
When do we apply DeMorgan's Law? Whenever we wish to “distribute” a negation over a logical connective; and, for internal naku negation, whenever a logical connective moves in to, or out of, the scope of a negation – when it crosses a negation boundary.
Let us apply DeMorgan's Law to some sample sentences. These sentences make use of forethought logical connectives, which are explained in Section 14.5. It suffices to know that ga and gi, used before each of a pair of sumti or bridi, mean “either” and “or” respectively, and that ge and gi used similarly mean “both” and “and”. Furthermore, ga, ge, and gi can all be suffixed with nai to negate the bridi or sumti that follows.
We have defined na and naku zo'u as, respectively, internal and external bridi negation. These forms being identical, the negation boundary always remains at the left end of the prenex. Thus, exporting or importing negation between external and internal bridi negation forms never requires DeMorgan's Law to be applied. Example 16.94 and Example 16.95 are exactly equivalent:
| la | djan. | na | klama | ga |
| that-named | John | [false] | goes-to | either |
| la | paris. | gi | la | rom. |
| that-named | Paris | or | that-named | Rome. |
| naku | zo'u | la | djan. | klama |
| It-is-false | that: | that-named | John | goes-to |
| ga | la | paris. | gi | la | rom. |
| either | that-named | Paris | or | that-named | Rome. |
It is not an acceptable logical manipulation to move a negator from the bridi level to one or more sumti. However, Example 16.94 and related examples are not sumti negations, but rather expand to form two logically connected sentences. In such a situation, DeMorgan's Law must be applied. For instance, Example 16.95 expands to:
| ge | la | djan. | la | paris. | na | klama | |
| [It-is-true-that] | both | that-named | John, | to-that-named | Paris, | [false] | goes, |
| gi | la | djan. | la | rom. | na | klama |
| and | that-named | John, | to-that-named | Rome, | [false] | goes. |
The ga and gi, meaning “either-or”, have become ge and gi, meaning “both-and”, as a consequence of moving the negators into the individual bridi.
Here is another example of DeMorgan's Law in action, involving bridi-tail logical connection (explained in Section 14.9):
| la | djein. | le | zarci | na | ge | dzukla | gi | bajrykla |
| that-named | Jane | to-the | market | [false] | both | walks | and | runs. |
| la | djein. | le | zarci | ganai | dzukla | ginai | bajrykla |
| that-named | Jane | to-the | market | either-([false] | walks) | or-([false] | runs. |
| that-named | Jane | to-the | market | if | walks | then-([false] | runs). |
(Placing le zarci before the selbri makes sure that it is properly associated with both parts of the logical connection. Otherwise, it is easy to erroneously leave it off one of the two sentences.)
It is wise, before freely doing transformations such as the one from Example 16.97 to Example 16.98, that you become familiar with expanding logical connectives to separate sentences, transforming the sentences, and then recondensing. Thus, you would prove the transformation correct by the following steps. By moving its na to the beginning of the prenex as a naku, Example 16.97 becomes:
| naku | zo'u | la | djein. | le | zarci |
| It-is-false-that | : | that-named | Jane | to-the | market |
| ge | dzukla | gi | bajrykla |
| (both | walks | and | runs). |
And by dividing the bridi with logically connected selbri into two bridi,
| naku | zo'u | ge | la | djein. | le | zarci | cu | dzukla |
| It-is-false | that: | both | (that-named | Jane | to-the | market | walks) |
| gi | la | djein. | le | zarci | cu | bajrykla |
| and | (that-named | Jane | to-the | market | runs). |
is the result.
At this expanded level, we apply DeMorgan's Law to distribute the negation in the prenex across both sentences, to get
| ga | la | djein. | le | zarci | na | dzukla |
| Either | that-named | Jane | to-the | market | [false] | walks, |
| gi | la | djein. | le | zarci | na | bajrykla |
| or | that-named | Jane | to-the | market | [false] | runs. |
which is the same as
| ganai | la | djein. | le | zarci | cu | dzukla |
| If | that-named | Jane | to-the | market | walks, |
| ginai | la | djein. | le | zarci | cu | bajrykla |
| then-([false] | that-named | Jane | to-the | market | runs). |
|
If Jane walks to the market, then she doesn't run. |
which then condenses down to Example 16.98.
DeMorgan's Law must also be applied to internal naku negations:
| ga | la | paris. | gi | la | rom. |
| (Either | that-named | Paris | or | that-named | Rome) |
| naku | se | klama | la | djan. |
| is-not | gone-to-by | that-named | John. |
| la | djan. | naku | klama | ge |
| that-named | John | doesn't | go-to | both |
| la | paris. | gi | la | rom. |
| that-named | Paris | and | that-named | Rome. |
That Example 16.103 and Example 16.104 mean the same should become evident by studying the English. It is a good exercise to work through the Lojban and prove that they are the same.
In addition to the variables da, de, and di that we have seen so far, which function as sumti and belong to selma'o KOhA, there are three corresponding variables bu'a, bu'e, and bu'i which function as selbri and belong to selma'o GOhA. These new variables allow existential or universal claims which are about the relationships between objects rather than the objects themselves. We will start with the usual silly examples; the literal translation will represent bu'a, bu'e and bu'i with F, G, and H respectively.
| su'o | bu'a | zo'u | la | djim. |
| For-at-least-one | relationship-F | : | that-named | Jim |
| bu'a | la | djan. |
| stands-in-relationship-F | to-that-named | John. |
|
There's some relationship between Jim and John. |
The translations of Example 16.105 show how unidiomatic selbri variables are in English; Lojban sentences like Example 16.105 need to be totally reworded in English. Furthermore, when a selbri variable appears in the prenex, it is necessary to precede it with a quantifier such as su'o; it is ungrammatical to just say bu'a zo'u. This rule is necessary because only sumti can appear in the prenex, and su'o bu'a is technically a sumti – in fact, it is an indefinite description like re nanmu, since bu'a is grammatically equivalent to a brivla like nanmu. However, indefinite descriptions involving the bu'a-series cannot be imported from the prenex.
When the prenex is omitted, the preceding number has to be omitted too:
As a result, if the number before the variable is anything but su'o, the prenex is required:
| ro | bu'a | zo'u | la | djim. |
| For-every | relationship-F | : | that-named | Jim |
| bu'a | la | djan. |
| stands-in-relationship-F | to-that-named | John. |
|
Every relationship exists between Jim and John. |
Example 16.105 and Example 16.106 are almost certainly true: Jim and John might be brothers, or might live in the same city, or at least have the property of being jointly human. Example 16.107 is palpably false, however; if Jim and John were related by every possible relationship, then they would have to be both brothers and father-and-son, which is impossible.
A variable may have a quantifier placed in front of it even though it has already been quantified explicitly or implicitly by a previous appearance, as in:
What does Example 16.108 mean? The appearance of ci da quantifies da as referring to three things, which are restricted by the relative clause to be cats. When re da appears later, it refers to two of those three things – there is no saying which ones. Further uses of da alone, if there were any, would refer once more to the three cats, so the requantification of da is purely local.
In general, the scope of a prenex that precedes a sentence extends to following sentences that are joined by ijeks (explained in Section 14.4) such as the .ije in Example 16.108. Theoretically, a bare i terminates the scope of the prenex. Informally, however, variables may persist for a while even after an i, as if it were an .ije. Prenexes that precede embedded bridi such as relative clauses and abstractions extend only to the end of the clause, as explained in Section 16.8. A prenex preceding tu'e…tu'u long-scope brackets persists until the tu'u, which may be many sentences or even paragraphs later.
If the variables da, de, and di (or the selbri variables bu'a, bu'e, and bu'i) are insufficient in number for handling a particular problem, the Lojban approach is to add a subscript to any of them. Each possible different combination of a subscript and a variable cmavo counts as a distinct variable in Lojban. Subscripts are explained in full in Section 19.6, but in general consist of the cmavo xi (of selma'o XI) followed by a number, one or more lerfu words forming a single string, or a general mathematical expression enclosed in parentheses.
A quantifier can be prefixed to a variable that has already been bound either in a prenex or earlier in the bridi, thus:
| ci | da | poi | prenu | cu | se ralju | pa | da |
| Three | Xs | which | are-persons | are-led-by | one-of | X |
|
Three people are led by one of them. |
The pa da in Example 16.109 does not specify the number of things to which da refers, as the preceding ci da does. Instead, it selects one of them for use in this sumti only. The number of referents of da remains three, but a single one (there is no way of knowing which one) is selected to be the leader.
This chapter is incomplete. There are many more aspects of logic that I neither fully understand nor feel competent to explain, neither in abstract nor in their Lojban realization. Lojban was designed to be a language that makes predicate logic speakable, and achieving that goal completely will need to wait for someone who understands both logic and Lojban better than I do. I can only hope to have pointed out the areas that are well-understood (and by implication, those that are not).